Notes on Proofs, Arguments, and Zero-Knowledge
Tags: machine learning, security, privacy, and mobile computing Guided by Liyao Xiang
 Image credit: Unsplash
Image credit: Unsplash
ZKP
Tags: machine learning, security, privacy, and mobile computing
Guided by Liyao Xiang
Proofs, Arguments, and Zero-Knowledge
https://people.cs.georgetown.edu/jthaler/ProofsArgsAndZK.html
1 Introduction
- (IPs) Interactive proofs
- (MIP) multi-prover interactive proof
- (PCP) orprobabilistically checkable proof
- (zk-SNARK) Zero-Knowledge Succinct Non-Interactive Argument of Knowledge)
2 Fingerprinting and Freivalds’ Algorithm
2.1 Reed-Solomon Fingerprinting
Reed-Solomon code可以看成对数据所产生的多项式。(见figure2-1) 哈希函数冲突的概率要小,否则影响可信度。
2.2 Freivalds’ algorithm
两个协议都将检查两个大对象(Reed-Solomon Fingerprinting中的向量,以及Freivalds算法中声称的答案矩阵和真实答案矩阵)的相等性的任务减少为检查这些对象的距离放大编码的单个随机条目的相等性。
2.3 拉格朗日插值公式
递推公式(2.10)
3 Definitions and Technical Preliminaries
3.1 IPs
error: $δ_c$ completeness error,$δ_s$ soundness error
交互式证明的开销因素:
- P的运行时间,V的运行时间,P的使用空间,V的使用空间,通信的比特总数,交换的消息总数
如果V和P交换k条消息,那么k/2的上界称为交互证明系统的轮复杂度
3.2 Argument Systems
- computational soundness
- reusability
- public verifiability
3.3 鲁棒性
为什么定义3.1认为$δ_c$和$δ_s$小于等于1/3: 出于方便或审美原因,不会对结果产生改变。
3.4 Schwartz-Zippel Lemma
d次多项式,最多有d个零点
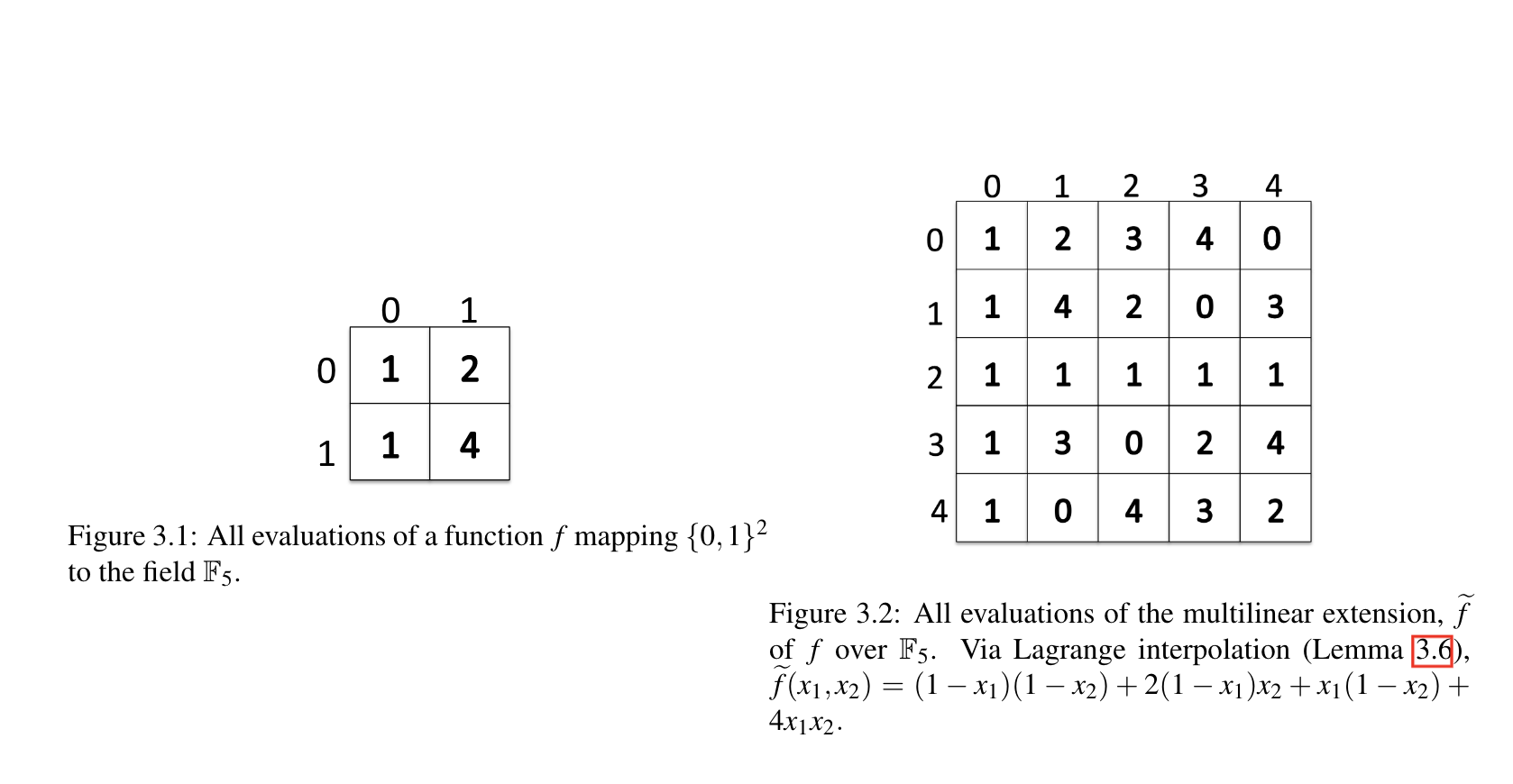
3.5 Low Degree and Multilinear Extensions
figure3.2 Lagrange interpolation 怎么用

4 IPs
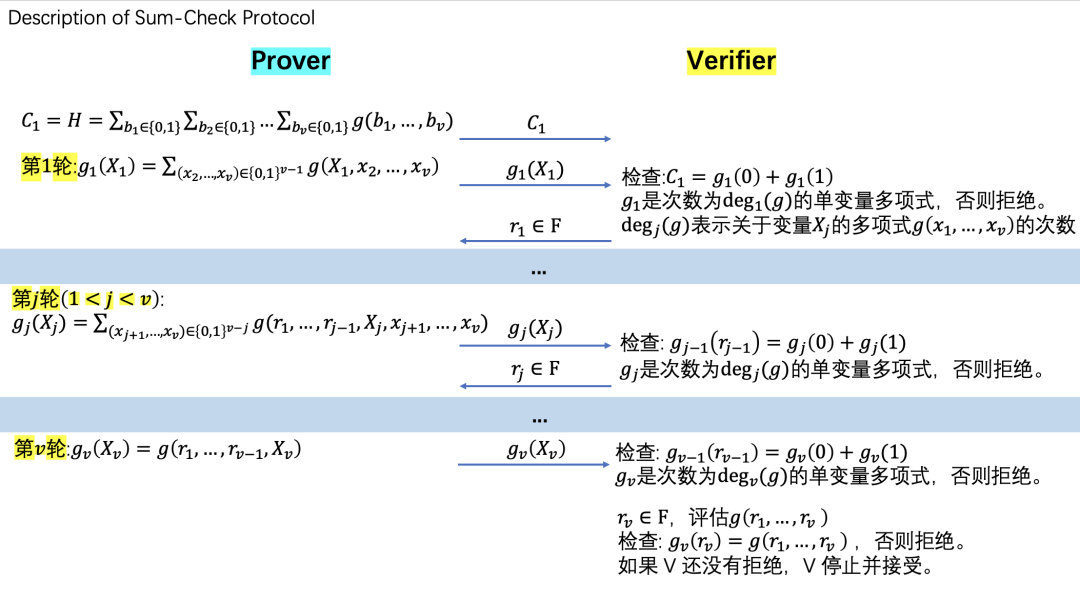
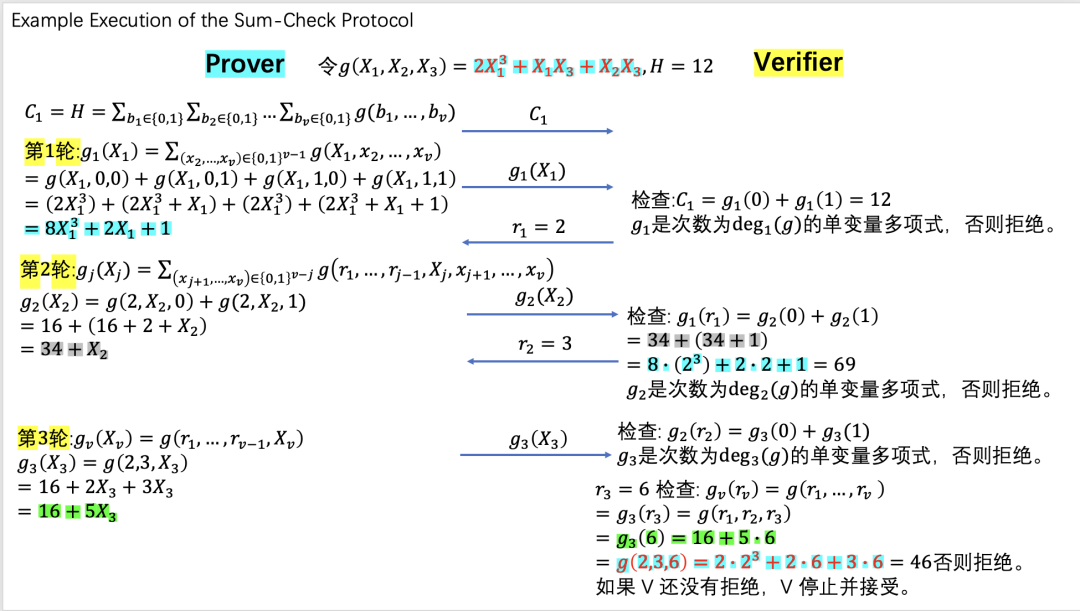
4.1 sum-check
算法解析:
4.2 SAT $\in$ IP
SAT问题即判断合取范式的可满足性 SAT协议非常接近IP = PSPACE:通过多项式时间验证者的交互式证明可解决的问题类别恰好等于多项式空间中可解的问题 doubly-efficient IPs
4.4 Third Application: Super-Efficient IP for MATMULT
本节描述了来自 [Tha13] 的用于矩阵乘法(matrix multiplication,MATMULT)的高度优化的 IP 协议。
给定域F上的两个n×n输入矩阵A,B,MATMULT的目标是计算矩阵乘积C=A·B。
和Freivalds协议相比:避免了P发送完整答案矩阵。
2.15
sec18-adi
MLaaS(服务即只能用于一个人)打上水印 方法:用backdoors (Pedersen commitment算法) open commitment过程:解密 commitment两个特性:binding,hiding bully proof set up-input-proof-verify Peng:介绍Peterson commitment算法,感兴趣的话看poly commitment ProofsArgsAndZK chapter14-16 Wu:ProofsArgsAndZK,看chapter10,重点是10.3
commitment
不解密隐私数据的情况下使用数据 过程:
- commit:对数据v,计算对应的承诺c,再把v和c发送给verify方
- open commitment:接收数据v,计算对应的承诺c’, 比较c和c'
两个特性:
- hiding:open commitment前,verify方不知道数据v
- binding:数据v与承诺c唯一对应
open commitment阶段可以使用zkp来完成,保护数据v。
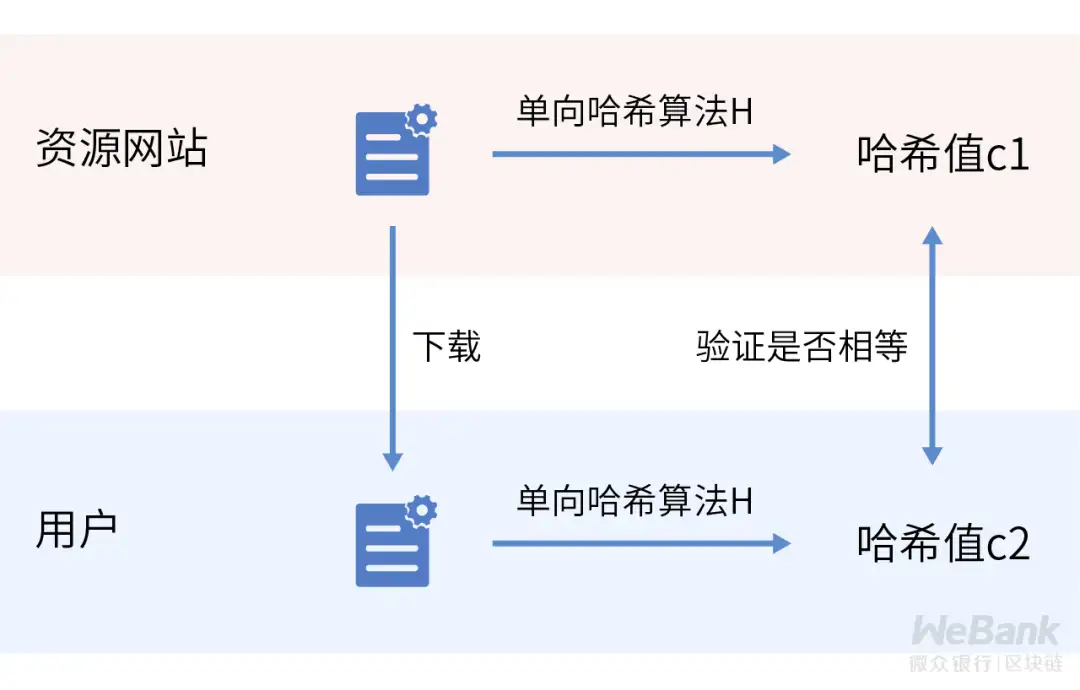
hash commitment
最简单的commitment
hash算法:单向=>hiding,不冲突=>binding
Pedersen commitment
算法 ProofsArgsAndZK 12.3 Protocol 5

cyclic group:循环群,定义为若一个群G的每一个元都是G的某一个固定元a的乘方,则称G为循环群,记作G=(a),a称为G的一个生成元(群是一种特殊的集合,元指元素)
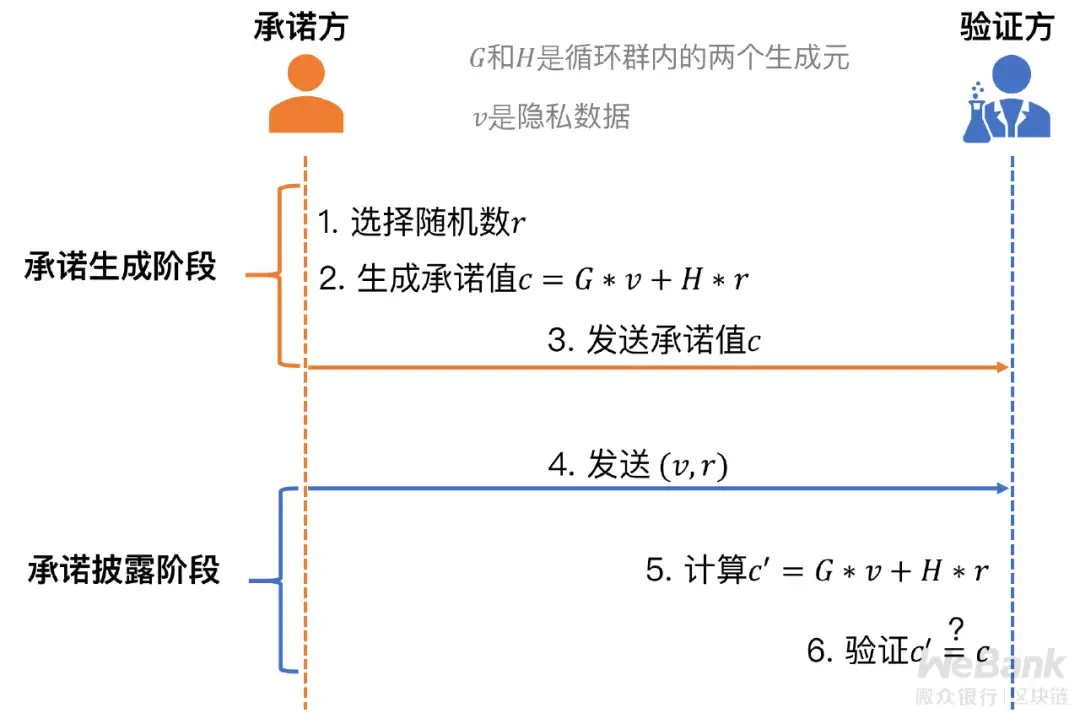
- 大数分解困难问题
- 给定两个大素数p和q,计算n=p*q是容易的。然而,给定n,求解p、q则是困难的。
- 离散对数困难问题
- 实数域,计算log2(9),用二分查找,很容易。
-
- 在模为n,生成元为g的有限域中,给定整数a,计算g^a = b是容易的。然而,给定b和g计算a则是困难的。(涉及有限域中的运算)
- 实数域,计算log2(9),用二分查找,很容易。
- 椭圆曲线上的离散对数困难问题
- 在有限域F上的椭圆曲线群,点P为曲线上某个点,给定整数a,计算a*P=Q是容易的。然而,根据P和Q计算a则是困难的。
Polynomial Commitment
2.18
watermarking-commitment and ZKP 1.数字水印在神经网络中的应用 2.数字水印与密码学工具(比如零知识证明)结合 A survey of deep neural network watermarking techniques A Systematic Review on Model Watermarking for Neural Networks
3.15
区块链-时间戳,歧义攻击 模型是公开的,验证是黑盒的(参数不公开) 基于计算资源的假设:攻击者不会花费过多的资源重训模型,不然开销太大。 trigle足够强,不能被反tune
